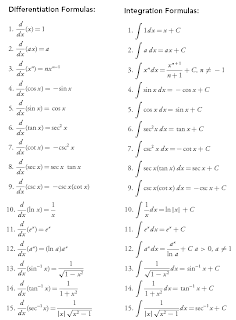Math special
Friday, 18 January 2013
Thursday, 17 January 2013
Slope
What is slope? If you have ever walked up or down a hill, then you have already experienced a real life example of slope
As you go up hill, you may feel like you are spending lots of energy to get yourself to move.
The steeper the hill, the harder it is for you to keep yourself moving

Keeping this fact in mind, by definition, the slope is the measure of the steepness of a line.
In real life, we see slope in any direction. However, in math, slope is defined from left to right.
I repeat we always measure slope going from left to right. This is very important!
There are three types of slope you can encounter. A slope can be positive, negative, or equal to zero. When the slope is equal to zero, we say that there is no slope
A positive slope:
If you go from left to right and you go up, it it a positive slope

A negative slope:
If you go from left to right and you go down, it it a negative slope

A zero slope:
If you go from left to right and you don't go up or down, it it a zero slope

The lesson about slope of a line or how to find the slope will explain what it means for a slope to ne positive, negative, or zero mathematically.
Continue your study of slope here in order
How to find the slope
Learn how to compute the slope using the rise and the run or 2 points
Undefined slope
A thorough explanation of what it means for a slope to be undefined
Graphing slope
Learn how to graph the slope using the slope and a point
Slope intercept form
Learn how to graph the slope using the slope and a point
Slope calculator
Given two points, this calculator will calculate the slope and the slope intercept form of a line
Related topics
Midpoint of a line segment
Find out how to find the midpoint of a line segment using the midpoint formula
Direct variation
A couple of real life examples of direct variation explained
Domain of a function
As you go up hill, you may feel like you are spending lots of energy to get yourself to move.
The steeper the hill, the harder it is for you to keep yourself moving
Keeping this fact in mind, by definition, the slope is the measure of the steepness of a line.
In real life, we see slope in any direction. However, in math, slope is defined from left to right.
I repeat we always measure slope going from left to right. This is very important!
There are three types of slope you can encounter. A slope can be positive, negative, or equal to zero. When the slope is equal to zero, we say that there is no slope
A positive slope:
If you go from left to right and you go up, it it a positive slope
A negative slope:
If you go from left to right and you go down, it it a negative slope
A zero slope:
If you go from left to right and you don't go up or down, it it a zero slope
The lesson about slope of a line or how to find the slope will explain what it means for a slope to ne positive, negative, or zero mathematically.
Continue your study of slope here in order
How to find the slope
Learn how to compute the slope using the rise and the run or 2 points
Undefined slope
A thorough explanation of what it means for a slope to be undefined
Graphing slope
Learn how to graph the slope using the slope and a point
Slope intercept form
Learn how to graph the slope using the slope and a point
Slope calculator
Given two points, this calculator will calculate the slope and the slope intercept form of a line
Related topics
Midpoint of a line segment
Find out how to find the midpoint of a line segment using the midpoint formula
Direct variation
A couple of real life examples of direct variation explained
Domain of a function
Integration
Integration :
This presentation concerns integration. I am not going to go through a long set of difficult manipulative examples, rather I want to raise important (as I see them) points I hope this will help people when preparing work programs and assessment instruments.
Until one does problems with applications in applied areas, the extension to topics in Mathematics C which concern integration will most likely concern freer use of the log, exponential and trigonometric functions, so a lot of what is here is relevant to Mathematics C too.
I want to make some points about
• indefinite integrals
• the definite integrals
• what is area
• the fundamental theorem of calculus
• simple substitution
• numerical integration
• manipulation packages
This presentation concerns integration. I am not going to go through a long set of difficult manipulative examples, rather I want to raise important (as I see them) points I hope this will help people when preparing work programs and assessment instruments.
Until one does problems with applications in applied areas, the extension to topics in Mathematics C which concern integration will most likely concern freer use of the log, exponential and trigonometric functions, so a lot of what is here is relevant to Mathematics C too.
I want to make some points about
• indefinite integrals
• the definite integrals
• what is area
• the fundamental theorem of calculus
• simple substitution
• numerical integration
• manipulation packages
Derivative:
Calculus is the mathematics of change, and the primary tool for studying change is a
procedure called differentiation. In this section, we shall introduce this procedure and
examine some of its uses, especially in computing rates of change. Here, and later in
this chapter, we shall encounter rates such as velocity, acceleration, production rates
with respect to labor level or capital expenditure, the rate of growth of a population,
the infection rate of a susceptible population during an epidemic, and many others.
Calculus was developed in the seventeenth century by Isaac Newton (1642–1727)
and G. W. Leibniz (1646–1716) and others at least in part in an attempt to deal with
two geometric problems:
Tangent problem: Find a tangent line at a particular point on a given curve.
Area problem: Find the area of the region under a given curve.
The area problem involves a procedure called integration in which quantities such as
area, average value, present value of an income stream, and blood flow rate are
computed as a special kind of limit of a sum. We shall study this procedure in Chapters
5 and 6. The tangent problem is closely related to the study of rates of change, and
we will begin our study of calculus by examining this connection.
Recall from Section 1.3 that a linear function L(x) mx b changes at the constant rate
m with respect to the independent variable x. That is, the rate of change of L(x) is given
by the slope or steepness of its graph, the line y mx b (Figure 2.1a). For a function
f(x) that is not linear, the rate of change is not constant but varies with x. In particular,
when x c the rate is given by the steepness of the graph of f(x) at the point P(c, f(c)),
which can be measured by the slope of the tangent line to the graph at P (Figure 2.1b).
The relationship between rate of change and slope is illustrate
Calculus is the mathematics of change, and the primary tool for studying change is a
procedure called differentiation. In this section, we shall introduce this procedure and
examine some of its uses, especially in computing rates of change. Here, and later in
this chapter, we shall encounter rates such as velocity, acceleration, production rates
with respect to labor level or capital expenditure, the rate of growth of a population,
the infection rate of a susceptible population during an epidemic, and many others.
Calculus was developed in the seventeenth century by Isaac Newton (1642–1727)
and G. W. Leibniz (1646–1716) and others at least in part in an attempt to deal with
two geometric problems:
Tangent problem: Find a tangent line at a particular point on a given curve.
Area problem: Find the area of the region under a given curve.
The area problem involves a procedure called integration in which quantities such as
area, average value, present value of an income stream, and blood flow rate are
computed as a special kind of limit of a sum. We shall study this procedure in Chapters
5 and 6. The tangent problem is closely related to the study of rates of change, and
we will begin our study of calculus by examining this connection.
Recall from Section 1.3 that a linear function L(x) mx b changes at the constant rate
m with respect to the independent variable x. That is, the rate of change of L(x) is given
by the slope or steepness of its graph, the line y mx b (Figure 2.1a). For a function
f(x) that is not linear, the rate of change is not constant but varies with x. In particular,
when x c the rate is given by the steepness of the graph of f(x) at the point P(c, f(c)),
which can be measured by the slope of the tangent line to the graph at P (Figure 2.1b).
The relationship between rate of change and slope is illustrate
Subscribe to:
Comments (Atom)